Bin Packing Algorithms
Introduction
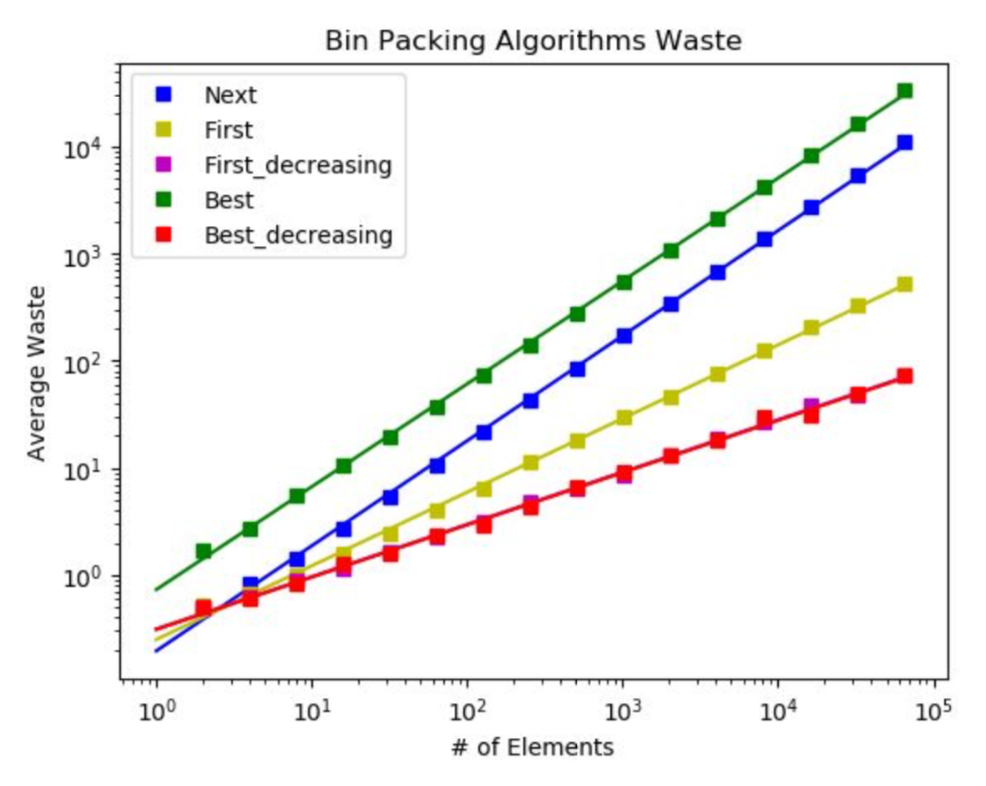
The goal for this project was to implement and test various bin packing algorithms in order to determine the quality of the solutions they produce. The bin packing problem attempts to find the most efficient, or waste-less, arrangement of values in a series of finite sized bins. There are many real world applications of this algorithm such as loading trucks, meeting weight capacities, and creating/storing file backups. I implemented 5 bin packing algorithms: Next Fit, First Fit, Best Fit, First Fit Decreasing, and Best Fit Decreasing. I will discuss my implementation, average waste, and conclusions drawn from each of these algorithms. I ran each algorithm 100 times on lists sized by a power of two up to n = 65,536. I plotted my data points and regression line on a log scaled plot. Additionally, I calculated the slope of the regression lines by taking the points at x = 1 and x = 65,536 for each graph and applied the slope formula. All algorithms were sanity checked and appear to be completely correct from empirical and visual analysis.
next Fit
This naive algorithm attempts to pack bins sequentially, never visiting previous bins to check for available room. The running time on this algorithm is O(n) as it makes a binary decision to either pack the value in the last bin or to create a new bin and pack it there for each of the n values. As we can expect the algorithms has high average waste. By taking the slope of the regression line, we can estimate W(A) as a function of n. The slope of the line is 0.1574 with a y-intercept of 0.1636, resulting in the function W(A) = 0.1574*n + 0.1636 for this algorithm.
First Fit
This greedy algorithm attempts to pack values in the first available bin, restarting its search at the beginning of the bin sequence for each value to be packed. The running time is O(n^2) because worst case there will be no room for any values and will either be placed in the final bin or create a new one. While this algorithm is much slower, it generates much less waste. The slope of the regression line for this algorithm is 0.008, with a y-intercept of 0.0041, resulting in the function W(A) = 0.008*n + 0.0041 for this algorithm. It is important to note that the number of bins used by the algorithm will never use more than twice the optimal number of bins. It is not possible for more than two bins to at most half full at any point in time, because those values would be packed together. This means that out of B bins, at least B-1 are more than half full, providing us with our optimal bounds for the algorithm.
First Fit Decreasing
This algorithm is implemented completely the same as First Fit, except the input is sorted in decreasing order before running the routine. To sort the input, I used my fastest implementation of Shell-sort from project 1. Sorting the input allows the algorithm to deal with the biggest values first, subsequently packing smaller values later in the process into pre-established almost filled bins. The idea is that many bins will be generated and filled with large values. When values to be packed reach a size of half the bin capacity or below, values will begin to be packed into the already created bins, occasionally creating more bins as the existing ones fill up. This results in much less waste as these smaller values are packed more efficiently. The slope of the regression line for this algorithm is 0.0011 with a y-intercept of 0.4971 resulting in the function W(A) = 0.0011*n + 0.4971. This algorithm generates much less waste than its non-decreasing counterpart.
Best Fit
This algorithm is by far the slowest of all the algorithms. This is because it iterates through the entire bin sequence and remembers the bin which had the least amount of room but could still pack the value. If the value could not fit anywhere, a new bin is added and the value is packed there. This leads the running time to be O(n^2), even in the best case. The idea for this algorithm is to pack bins as tightly as possible, ensuring that waste is minimized on each packing of a value. However, this packing algorithm generated the most waste of any algorithm so far. I believe this to be a result of the algorithm filling bins very tightly, not allowing any room for values larger than half capacity and resulting in higher than expected waste. The waste function for this algorithm is W(A) = 0.4679*n + 0.7388.
Best fit Decreasing
This algorithm is implemented completely the same as Best Fit, except the input is sorted in decreasing order before running the routine. To sort the input, I used my fastest implementation of Shell-sort from project 1. This version of the algorithm performs much better with a waste function of W(A) = 0.0011*n + 0.5. This is because the algorithm deals with all of the largest values first and then can more efficiently pack in the smaller values that will follow. Once the algorithm reaches values of half the bin capacity size, it can start packing those values into already created bins. This “order of operations” makes the packing much less wasteful.
Conclusions
Based on my empirical results, I would rank the bin packing algorithms, from least to most wasteful, as follows.
Best Fit Decreasing | | First Fit Decreasing
First Fit
Next Fit
Best Fit
Best Fit Decreasing and First Fit Decreasing both perform at the nearly same level with identical regression slopes. First Fit performs fairly well and put a good attempt towards keeping up with its decreasing counterpart. Finally we have Next Fit which barely outperforms the Best Fit algorithm. However, as far as I am aware, Best Fit should rank higher than First Fit meaning there could be an error in my algorithm implementation or testing infrastructure.